Strong Interactions and the Missing Mathematical Toolkit

The core hypothesis that a white hole powers the expansion of a bulk upon the exterior surface of which our universe resides has important consequences for the WHD program’s choice of mathematical toolkit and research methodology. For one, the birth and evolution of our universe must be modeled as an emergent order parameter in a cascade of open and nonlinear dynamical systems held far from equilibrium ultimately by the negative mass at the white hole core. The need to obtain insight into strongly coupled dynamics in both bulk and boundary becomes absolutely critical. The failure to do so makes it impossible for the research program even to get off the ground.

One of the greatest accomplishments of gauge/gravity or AdS/CFT duality is in its methodological success in opening up, albeit to a limited extent, the strong coupling regimes of certain quantum field theories. Many are now cautiously placing their hopes in holographic renormalization as a key tool to lift the veil of our ignorance regarding strong interactions. The question naturally arises – could holography bring a toolkit to bear in getting the WHD program off the ground?

In this section, we first explore some of the similarities and differences between holography in AdS/CFT toy models and the cosmological narrative of the WHD program. Then we begin to train our intuition on how strong interactions work in nature and whether our conceptual understanding of strong interactions is itself adequate. Finally, this section makes a rather poor attempt at urging a more radical approach to rethinking our mathematical toolkit as we begin to explore a universe that is fundamentally emergent, slaved, open and metastable.

Motivating our desire to radically rethink our math is not only the belief that we lack the tools to model strong interactions in the WHD program realistically; rather, our very conceptualization of the nature of these strong interactions also seems to be deficient. Making an approach goes beyond simply accepting the abandonment of quasiparticle descriptions and Lagrangians – beyond just looking for the right geometry and nonlinear partial differential equations in the bulk – since the bulk not only interacts strongly, but rather than relaxing out of that regime, it is held there for an extremely long period of time by a continuous source of external energy and a complex set of causal relationships. Indeed, the very nature of causality that we take for granted in our physics will require modification in the end.

But let’s start with toy model holography and note some obvious differences when compared to the WHD program. First, unlike the AdS/CFT correspondence or gauge/gravity duality generally, in WHD holography, the behavior in both the bulk and the exterior boundary surface can be strongly coupled at certain energy scales. Indeed, the higher-dimensional bulk likely remains strongly coupled during almost the entire lifetime of our universe, while the lower-dimensional exterior surface can exhibit strong interactions too, e.g., QGP at a temperature on the order of 1012 K (or, for instance, the numerous types of strong interactions resulting in complex forms of matter and, ultimately, life).

Second, and related to the above, WHD holography is not expected to be a true mirror as in gauge/gravity holography where the QFT on the boundary can be mirrored precisely by the gravity in the bulk. In fact, in the WHD program, much of what happens on the boundary exterior is decoupled from the far-from-equilibrium dynamics in the bulk on the timescales we care about. To the extent a 1:1 encoding exists between the bulk and the exterior boundary, it is not a true mirror, but rather a kind of slaving mechanism in which the phase space of the boundary and the journey through that phase space are determined by a control parameter residing in the bulk. We can tell you what can and cannot happen on the boundary by looking at the bulk, but what happens in the boundary is not the same thing happening in the bulk.

Third, in WHD holography, we find the same spin-2 graviton in both the higher-dimensional bulk and the lower-dimensional exterior boundary surface. In this sense, we cannot really describe gravity in the lower-dimensional spacetime as emergent out of the local field theory on the boundary. However, we can explain the relative weakness of gravity in the lower-dimensional spacetime.

Fourth, WHD holography incorporates white holes and negative mass, two physical concepts that are currently seen as unrealistic by most physicists. The modifications required to holographic renormalization by incorporating these two concepts could be significant. That said, the WHD program can still be viewed as relying upon a black hole to obtain the benefits of a thermodynamics governed by an area law. Although there is nothing in principle that would prevent a white hole from serving this role, recall that in the WHD program the Big Bang event occurs out of a primordial black hole vent dissipating the energy of the far-from-equilibrium dynamics driven by the white hole in the bulk. In this sense, the WHD program preserves much of the basic framework of holography. However, the benefits in gauge/gravity holography of an area law for thermodynamic properties may not apply in the WHD program. For instance, there is no requirement or expectation of global entropy equivalence between the higher-dimensional bulk and lower-dimensional exterior boundary surface. In fact, the low-entropy behavior of the bulk requires high entropy behavior on the exterior boundary surface.

Fifth, the boundary surface in WHD holography is a hydraulic jump with complex interactions affecting both its interior and exterior surfaces, which is very different from the simple d-dimensional surface on which a conformal field theory is built in AdS/CFT holography.

Taking all of this into account, it could be argued that gauge/gravity duality has absolutely nothing to do with the cosmological narrative of the WHD program. From a practitioner’s standpoint, this may be obviously true. However, taking a step back, AdS/CFT and WHD holography share a number of important features. First, they both enable a dramatic reduction in degrees of freedom due to collective behavior arising out of a kind of slaving of many components under the influence of an environmental parameter driving the system. This characteristic is what enables a window into strong coupling behavior.

Second, the concepts around how the bulk geometric interactions encode boundary interactions are similar. For instance, in both holographies the interactions at the boundary of the bulk specify the local interactions (UV scale) on the exterior boundary surface, while the interactions towards the inner region of the bulk determine the global interactions (IR scale) on the exterior boundary surface.

Third, like AdS/CFT, WHD holography predicts the existence of nearly ideal fluids and the need to better understand their remarkable properties. For instance, in the WHD program, we would expect the positive and negative mass fluids in the bulk spacetime to have a shear viscosity to entropy density ratio (η/s) that is extremely low, i.e., on the order of the Gauss-Bonnet lower bound of 1/4π(16/25) or perhaps some (significant?) correction to it based on the presence of negative mass, even though the entropy of the far-from-equilibrium dynamics of the fluids in the bulk is low.

It is worth noting that these similarities between AdS/CFT and WHD holography discussed above are generally features of systems held far from equilibrium – large number of system components, emergent collective behavior, dramatic reduction in degrees of freedom, inapplicability of deterministic and integrable trajectory dynamics and resulting lack of analytic solutions, highly non-ergodic journey of a system through its phase space – these are all hallmarks of systems that are influenced from the outside in a manner that prevents the system’s components from ever reaching a free state. In this sense, the encoding of local interactions on a boundary, which is typically the language used by holographists, could be more accurately reformulated as a kind of slaving of a system by its environment. Put simply, what holographists refer to as an encoding process is just looking through a glass darkly at a slaving process.

To be clear, there are countless systems in nature that exhibit equilibrium, near equilibrium or tending-toward equilibrium dynamics. This is equivalent to saying that there are many real systems that exist within deep potential wells with dynamics uncoupled temporarily to the slaving dynamics of their parent systems on the timescales relevant to our inquiry. Thus, it is obviously not fair to say that all real systems should be modeled from the standpoint of far from equilibrium methods for all purposes. That is an absurd proposition.

However, the systems we care about at cosmological and quantum scales are generally operating in nature as far-from-equilibrium systems. That we can destroy or alter that natural far-from-equilibrium context in the real world and in lab experiments does not diminish this fact. You can always find a time scale at which a closed system is an open system. Our understanding of nature at the present time, while very thorough for closed systems, is severely lacking in the treatment of open, far-from-equilibrium systems at the cosmological and quantum scale. To the extent we care that science generates insight and explanatory power concerning the nature of our physical reality, we ignore these background truths at our peril.

The approach of modern physics has always been to start easy and then try to correct to hard. That approach has engendered tremendous insight into aspects of nature that would otherwise have remained entirely inaccessible to us. It has provided the backbone of our understanding of the universe and the foundation of all technological advancement for centuries now. It is not our intent to undermine all of that progress but rather to appreciate that the approach is not without cost.

Building up a picture of reality over many generations based on closed systems, integrable dynamics, deterministic trajectories, linear causality, inert matter, randomly and freely interacting particles, and analytically solvable equations is almost certainly stifling our mathematical imagination – an imagination we need now more than ever. What was once the foundation of our progress is arguably now a crutch holding us back.

In fairness, any proclamation about the inadequacy of our current mathematical toolkits amounts to nothing more than a check that is easy to write but hard to cash. One of the most exciting aspects of holography is that it gives us access into strongly interacting dynamics, albeit for systems that are nowhere found in nature as far as we know. This progress nonetheless offers a glimmer of hope to overcome the fundamental limitations of perturbation theory, lattice theory and other traditional techniques when applied to the questions we think are most important to answer. Other tools like fluid dynamics enable us to make an approach to certain strongly interacting systems as well. It just feels like something less incremental, something much more radical, will be required than what is currently on offer.

That suspicion rests in significant part on the belief that our current conceptual understanding of strong interactions, e.g., as understood by classical supergravity theories, fluid dynamics approximations or quantum chaos applications in lattice theory, may not capture all of the features associated with strong coupling dynamics that nature actually employs into its service. In order even to make an approach around developing a new mathematical toolkit, it may be worthwhile to train our intuition. Let’s do that in two ways.

First, we might ask why holography is in fact successful at developing an accessible formal description of strongly coupled dynamics for any system at all, even if they’re not ones we encounter in nature. Let’s take, for example, attempting to generate the renormalization group (RG) flow of a quantum field theory without being able to generate an explicit beta function because we are dealing with a complex, strongly coupled system. Holography offers a neat mathematical trick to overcome this problem by treating the RG coarse-graining as a d+1 dimensional lattice and the original UV lattice of the system as the d-dimensional boundary. The d+1-dimensional field has the same charges, tensor structure and other quantum numbers as the d-dimensional coupling. Each scalar operator is matched to a bulk scalar field, each current operator corresponds to a bulk vector field. The canonical stress-tensor has a canonical spin-2 field in the bulk spacetime which must either couple universally or decouple at low energies.

Critically, for this mathematical trick to work such that the RG bulk is equivalent to the UV lattice, two things have to be true: (i) it has to be possible to coarse-grain the UV lattice without losing the properties encoded in it; and (ii) the bulk must have the properties of a black hole to ensure that (a) the entropies of the two spacetimes are the same, which can only happen if the entropy of the bulk responds to an area law, and (b) the beta-function can be uniquely determined in the bulk by virtue of the black hole providing a physical justification for eliminating one of the two solutions.

In other words, the success of holography depends upon the ability to encode local properties globally and the presence of a higher-dimensional spacetime that thermodynamically responds to an area law. If we have a traceless, conserved energy-momentum tensor on the boundary, then when we integrate Einstein’s equations in the bulk to obtain the corresponding bulk geometry—that geometry is a black hole. In other words, this is not an assumption that we choose in the theory; it is the result of a computation based on sound first principles.

Why is this so? It is perhaps all too convenient to speculate that the math finds a black hole on the other side of the quantum field theory because that is what’s on the other side of fundamental fields permeating our universe. But would that convenience make it any less true? Further, building a holography from the RG flow may work precisely because far-from-equilibrium dynamics holds at the most global scale, and thus the kind of coarse-graining entailed by the RG dimension is what in fact is occurring in nature by virtue of the white hole control parameter holding those UV scale components far from equilibrium.

Iteratively coarse-graining the lattice from the UV scale up to the IR scale, in which each higher lattice vertex becomes an average of lower-level vertices, while preserving the vacuum and low energy excitations of the original lattice, can generate a beta-function that is still local in scale. The local and global are intimately interwoven. This is perhaps the hallmark characteristic of systems held far from equilibrium by an external energy source.

We must then ask: what is the actual nature of the interaction between a locally specified component of a system, e.g., a spin on a lattice, and the global properties of that system? The nature of this interaction is fundamentally open, nonlinear, nonintegrable, probabilistic and indeterministic. This is the only perspective from which we can provide any explanation for the complexity, self-organization, spontaneity, nonlocality, entanglement and, in general, for the remarkable combination of chaotic and orderly behavior, that a wide range of disciplines are increasingly recognizing must be attributed to matter at every level of its analysis.

The WHD program contends that the primary cause of this seemingly inherent capability of matter rests in the concept of circular causality that dominates the evolution of any system in which many components are held far from an equilibrium state. Under certain conditions, i.e., where a system may be described as closed or as achieving or approaching equilibrium, circular causality reduces to linear causality. However, for most real systems in nature, the assumption of linear causality results in a failure to capture critical features of the system. For these systems, our mathematical models must respect the circularly causal nature of the system’s interactions, which are always governed by the following tripartite scheme.

1. Control Parameter (CP): the environment or power source that drives the system from the outside and shapes the phase space of all relevant state variables;

2. Components (COMP): a large quantity of individual constituents acted upon and held far from equilibrium by the control parameter. Components traverse the phase space in an indeterminate, probabilistic manner and can exhibit interactions ranging from extremely weak to extremely strong depending in the first instance upon the behavior of the control parameter. When interactions are extremely weak, circular causality will decay into linear causality. When interactions are extremely strong, the components will traverse the phase space in a highly non-ergodic manner and generate nonlocal qualitative changes in the emergent order parameter;

3. Order Parameter (OP): the emergent ‘reality’ generated by the collective behavior of components under strong interactions, which is qualitatively greater than and different from a mere linear summing of the component parts. The order parameter exhibits its own causal agency separate and apart from the components and acts back on the components and on the control parameter resulting in a complex feedback loop of interactions which we generally refer to as circular causality.

In metastable regimes operating under this complex feedback loop of interactions, changes in the control parameter or order parameter, or spontaneous fluctuations in any of the many components, have the potential to drive the system towards qualitative changes in the behavior of the order parameter based on the system’s natural tendency to maximize its degrees of freedom, which requires increased compression of the information embodied in the system components. This is what we really mean when we talk about strong interactions.

The nature of the interaction is extremely complex, as described by the arrows in the diagram below showing how the causal agents act on and back on one another.

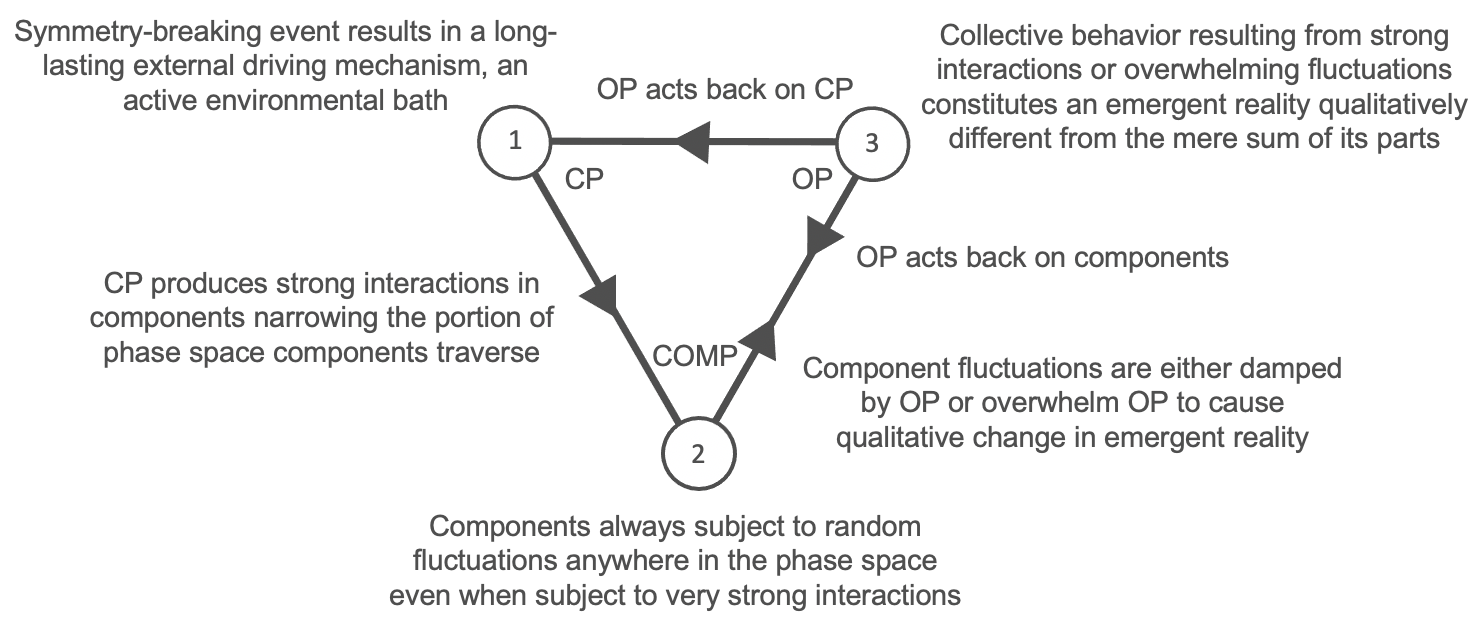
This is the process that drives spontaneous symmetry-breaking and the creation of new forms of organized matter in which the order parameter at an earlier evolutionary level now serves as the control parameter for the next level of the emergent reality. This is what is meant by modeling the universe as embedded within a cascade of emergent order parameters exhibiting circular causality at each evolutionary step.

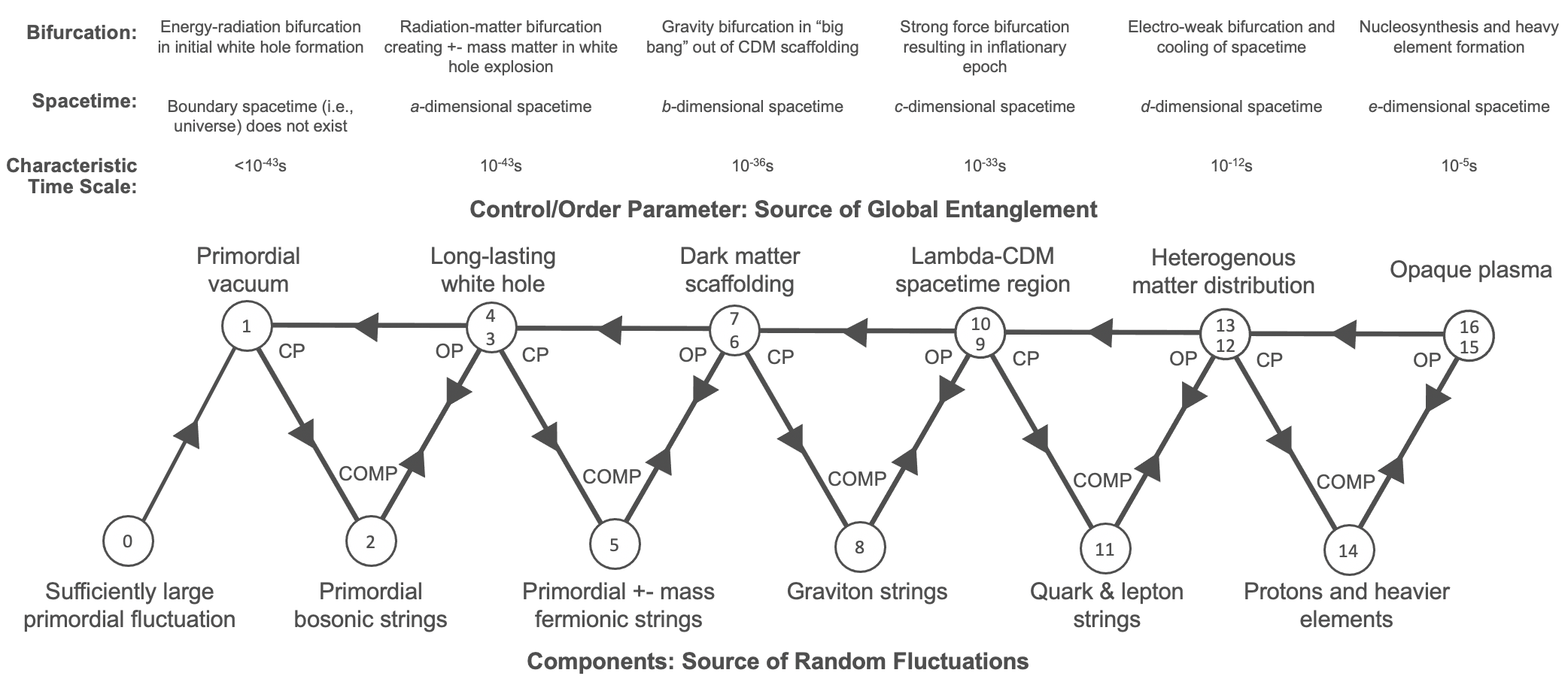
A highly simplified cartoon diagram of this emerging cascade is depicted below simply to illustrate the concept that underlying the seemingly linear evolution of the cosmos, a circularly causal mechanism establishes a global (i.e., fundamentally nonlocal) relationship among all components within any given level, as well as a complex causal relationship across the different levels.

A consequence of this model is that, at certain evolutionary levels, circular causality enables interactions between the global state of a field and the localized excitations of the field’s excess energy that from our perspective would appear to be non-spatially-mediated and non-temporally-mediated. These interactions could occur instantaneously and at arbitrary distances assuming the strong interactions that couple the components to the field aren’t otherwise broken from the outside. These strong interactions that slave each of the field’s excitations (i.e. particles) to the directives of the control parameter and the order parameter (i.e. the field) are characteristic of natural systems.

No violation of special relativity’s requirement that photons establish a speed limit on signals would be required because the signals here are not propagating locally through space, at least not the space of special relativity. On this view, space and time are themselves emergent properties of the circularly causal feedback loop. The tick of the arrow of time is defined as the characteristic time it takes to complete one loop comprised of these circularly causal effects whereby the control parameter acts on the components, the components act on themselves, one another (self-interaction effects) and on the order parameter, and the order parameter acts back on the control parameter and components. This kind of complex interaction cannot be modeled analytically in any meaningful sense but perhaps can be approximated numerically.

The switching time for any qualitative change of the system, for instance at a bifurcation (i.e., symmetry-breaking event), would be on the order of the characteristic time and would thus be instantaneous for any systems whose characteristic time scale is faster than the speed of a photon through vacuum space. Far from being weird or spooky, instantaneous “communication” at long distances becomes one of the most natural results one might expect from a reality that is constituted via circularly causal interactions with a fully emergent and relational spacetime.

The characteristic time scale of interactions that occur on the boundary is the Planck time, ~10-43, but the characteristic time scale in the bulk must therefore be some shorter time scale. The Planck scale does indeed represent a fundamental discrete pixilation of reality on the boundary, a maximum theoretical limit to the time-step of the evolution of our boundary-trapped universe. However, any interactions and excitations that reside in the bulk would evolve on a shorter characteristic time scale.

The degrees of freedom of the space are determined by the vibrational, rotational and/or translational motion of the components, which is governed mainly by the potential established by the control parameter holding those components far from equilibrium (which nonetheless always remains subject to random fluctuations from any component even under the strongest of potentials). Space is thus a fully relational concept emerging out of the collective response of many components to the potential landscape maintained by the control parameter.

In a literal sense, each level of this cascade of circularly causal feedback loops generates its own emergent spacetime. The order parameter of an earlier evolutionary level serves as a control parameter of a subsequent evolutionary level, establishing a link across the spacetimes, but the spacetime at one level is not actually “experienced by” the components of another level. From the perspective of those components, it doesn’t exist. However, modifying the potential landscape at one level perturbs not just the components on that level, but in principle could perturb earlier or later evolutionary levels as well. If the perturbation is strong enough, the stability regimes at those other levels may undergo a transformation as a result of a fluctuation that cascades from an entirely different level of the interconnected spacetimes. In other words, the components of each level may be “ignorant” of the spacetimes at any of the other levels, but changes in the stability of the spacetime at any level could cascade to affect or destroy the spacetimes at the other levels.

Models must be developed for each level of the cascade. The fundamental control parameter driving the entire system is the negative mass at the white hole core, driving the many positive and negative mass excitations in the bulk.

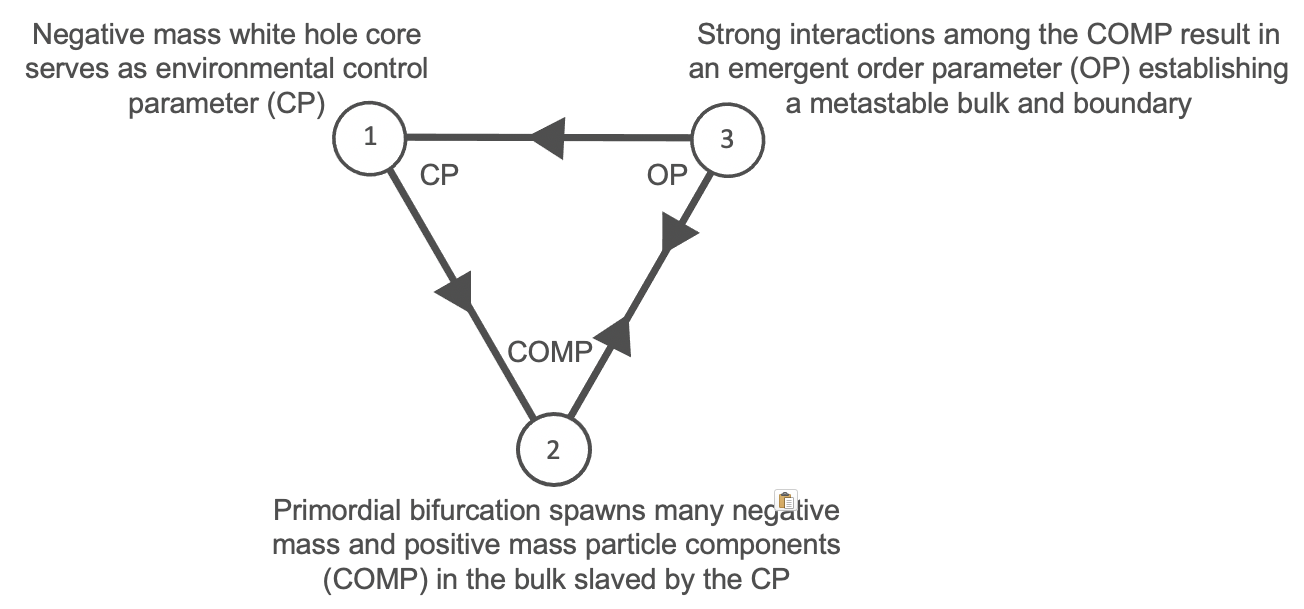
By modeling the boundary of the bulk as an open nonlinear dynamical system emerging out of the slaving of the positive and negative mass excitations by the white hole core, we are thus required to model the universe itself in similar fashion, as an emergent order parameter slaved by the boundary conditions. Thus, while the boundary conditions serve as an emergent order parameter at the level of the white hole formation and expansion (“Simplified Level 1”), they now serve as a control parameter at the subsequent evolutionary level, generating the emergent order parameter we call the universe (“Simplified Level 2”).

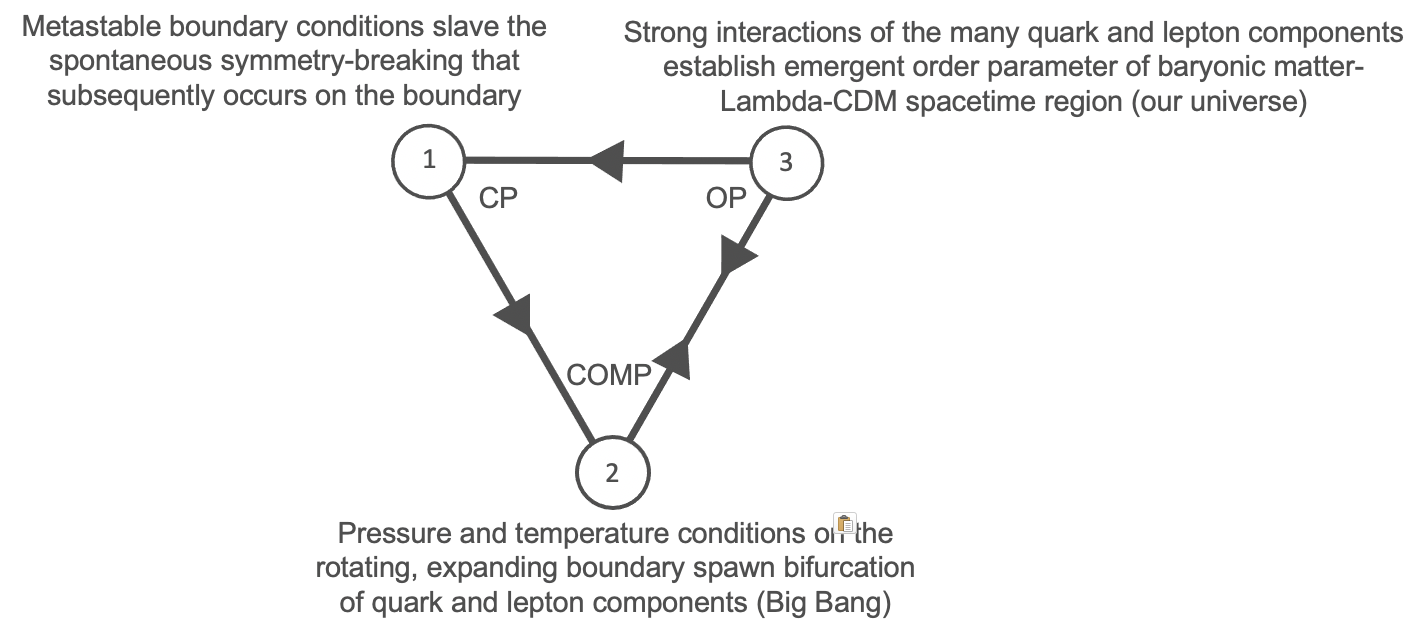
These circular causality diagrams reflect both a fundamental substantive claim about how nature works and an important stake in the ground about the research methodology employed in the WHD program. In essence, the WHD program treats linear causality, which serves as the foundation for much of theoretical physics and our commonsense view of reality, as a coarse-grained approximation of a much more subtle circular causality that permeates every level and feature of existence.

This concept of circular causality and the tripartite scheme of complex interactions suggests that our very understanding of strong interactions via coupling constants in Hamiltonians and Lagrangians represents a debased and distorted view of how nature works. It is an open question whether the recent interest in developing the Lindbladian formalism for open, driven systems can do the job, or whether something even more radical is required to model the basic properties and circularly causal evolution of each system level. This will be explored in the next chapter.